- 824.00 KB
- 35页
- 1、本文档共5页,可阅读全部内容。
- 2、本文档由网友投稿或网络整理,如有侵权请及时联系我们处理。
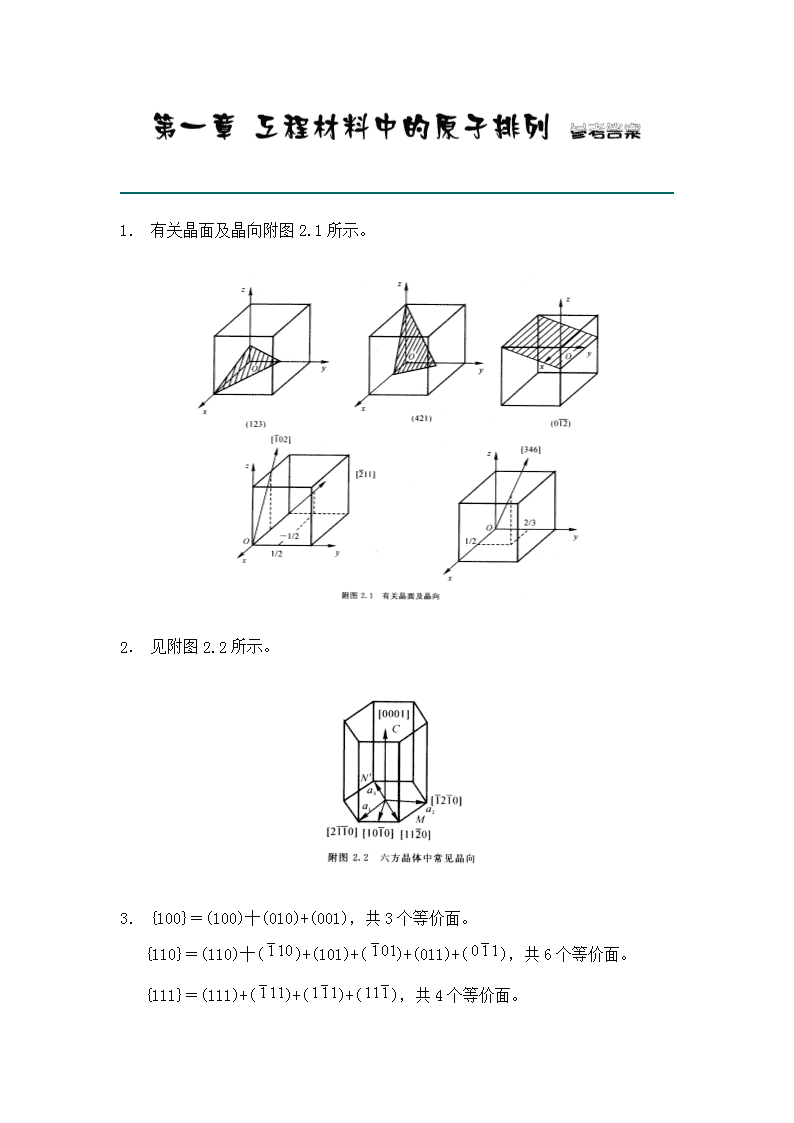
'1. 有关晶面及晶向附图2.1所示。2. 见附图2.2所示。3. {100}=(100)十(010)+(001),共3个等价面。{110}=(110)十()+(101)+()+(011)+(),共6个等价面。{111}=(111)+()+()+(),共4个等价面。
共12个等价面。4. 单位晶胞的体积为VCu=0.14nm3(或1.4×10-28m3)5. (1)0.088nm;(2)0.100nm。6. Cu原子的线密度为2.77×106个原子/mm。Fe原子的线密度为3.50×106个原子/mm。7. 1.6l×l013个原子/mm2;1.14X1013个原子/mm2;1.86×1013个原子/mm2。8. (1)5.29×1028个矽原子/m3; (2)0.33。9. 9.0.4×10-18/个原子。10. 1.06×1014倍。11. (1)这种看法不正确。在位错环运动移出晶体后,滑移面上、下两部分晶体相对移动的距离是由其柏氏矢量决定的。位错环的柏氏矢量为b,故其相对滑移了一个b的距离。(2)A"B"为右螺型位错,C"D"为左螺型位错;B"C"为正刃型位错,D"A"为负刃型位错。位错运动移出晶体后滑移方向及滑移量如附图2.3所示。12. (1)应沿滑移面上、下两部分晶体施加一切应力τ0,的方向应与de位错线平行。(2)在上述切应力作用下,位错线de将向左(或右)移动,即沿着与位错线de垂直的方向(且在滑移面上)移动。在位错线沿滑移面旋转360°后,在晶体表面沿柏氏矢量方向产生宽度为一个b的台阶。
13. (1),其大小为,其方向见附图2.4所示。(2)位错线方向及指数如附图2.4所示。14. (1)能。几何条件:∑b前=∑b后=;能量条件:∑b前2=>∑b后2=(2)不能。能量条件:∑b前2=∑b后2,两边能量相等。(3)不能。几何条件:∑b前=a/b[557],∑b后=a/b[11¯1],不能满足。(4)不能。能量条件:∑b前2=a2 <∑b后2=,即反应后能量升高。15. (1)能够进行。因为既满足几何条件:∑b前=∑b后=,又满足能量条件:∑b前2=>∑b后2=(2)b合=;该位错为弗兰克不全位错。16. (1)假设晶体中位错线互相缠结、互相钉扎,则可能存在的位错源数目个/Cm3。(2)τNi=1.95×107Pa。
17. 当θ=1°,D=14nm;θ=10°,D=1.4nm时,即位错之间仅有5~6个原子间距,此时位错密度太大,说明当θ角较大时,该模型已不适用。18. 畸变能是原来的0.75倍(说明形成亚晶界后,位错能量降低)。 19. 设小角度晶界的结构由刃型位错排列而成,位错间距为D。晶界的能量γ由位错的能量E构成,设l为位错线的长度,由附图2.5可知,由位错的能量计算可知,取R=D(超过D的地方,应力场相互抵消),r0=b和θ=b/D代入上式可得:式中
20. (1)晶体点阵也称晶体结构,是指原子的具体排列;而空间点阵则是忽略了原子的体积,而把它们抽象为纯几何点。(2)密排六方结构。(3)原子半径发生收缩。这是因为原子要尽量保持自己所占的体积不变或少变[原子所占体积VA=原子的体积(4/3πr3+间隙体积],当晶体结构的配位数减小时,即发生间隙体积的增加,若要维持上述方程的平衡,则原子半径必然发生收缩。(4)不能。因为位错环是通过环内晶体发生滑移、环外晶体不滑移才能形成。(5)外力在滑移面的滑移方向上的分切应力。(6)始终是柏氏矢量方向。(7)位错的交割。(8)共格界面。(9)否,扭转晶界就由交叉的同号螺型位错构成。1. 其比较如附表2.1所示。附表2.1 间隙固溶体与间隙化合物的比较类 别间隙固熔体间隙化合物相同点一般都是由过渡族金属与原子半径较小的C,N,H,O,B等非金属元素所组成 不同点晶体结构属于固熔体相,保持熔剂的晶格类型属于金属化合物相,形成不同于其组元的新点阵表达式用α、β、γ等表示用化学分子式MX,M2X等表示机械性能强度、硬度较低,塑性、韧性好高硬度、高熔点,甥性、韧性差2. 有序固熔体,其中各组元原子分别占据各自的布拉菲点阵——称为分点阵,整个固熔体就是由各组元的分点阵组成的复杂点阵,也叫超点阵或超结构。
这种排列和原子之间的结合能(键)有关。结合能愈大,原子愈不容易结合。如果异类原子间结合能小于同类原子间结合能,即EAB<(EAA十EBB)/2,则熔质原子呈部分有序或完全有序排列。有序化的推动力是混合能参量(εm=εAB-1/2(EAA+EBB))εm<0,而有序化的阻力则是组态熵;升温使后者对于自由能的贡献(-TS)增加,达到某个临界温度以后,则紊乱无序的固熔体更为稳定,有序固熔体消失,而变成无序固熔体。3. 在原子尺寸因素相近的情况下,上述元素在Ag中的固熔度(摩尔分数)受原子价因素的影响,即价电子浓度e/a是决定固熔度(摩尔分数)的一个重要因素。它们的原子价分别为2,3,4,5价,Ag为1价,相应的极限固熔度时的电子浓度可用公式c=ZA(1一xB)+ZBxB计算。式中,ZA,ZB分别为A,B组元的价电子数;xB为B组元的摩尔分数。上述元素在固溶度(摩尔分数)极限时的电子浓度分别为1.43,1.42,1.39,1.31。4. Α-Fe为体心立方点阵,致密度虽然较小,但是它的间隙数目多且分散,因而间隙半径很小:r四=0.291,R=0.0361nm;r八=0.154,R=0.0191nm。H,N,C,B等元素熔人。α-Fe中形成间隙固熔体,由于尺寸因素相差很大,所以固熔度(摩尔分数)都很小。例如N在α-Fe中的固熔度(摩尔分数)在590℃时达到最大值,约为WN=0.1/l0-2,在室温时降至WN=0.001/l0-2;C在α-Fe中的固溶度(摩尔分数)在727℃时达最大值,仅为WC=0.02l8/10-2,在室温时降至WC=0.006/10-2。所以,可以认为碳原子在室温几乎不熔于α-Fe中,微量碳原子仅偏聚在位错等晶体缺陷附近。假若碳原子熔入。α-Fe中时,它的位置多在α-Fe的八面体间隙中心,因为。α-Fe中的八面体间隙是不对称的,形为扁八面体,[100]方向上间隙半径r=0.154R,而在[110]方向上,r=0.633R,当碳原子熔入时只引起一个方向上的点阵畸变。硼原子较大,熔人间隙更为困难,有时部分硼原子以置换方式熔人。氢在α-Fe中的固熔度(摩尔分数)也很小,且随温度下降时迅速降低。以上元素在γ-Fe。中的固熔度(摩尔分数)较大一些。这是因为γ-Fe具有面心立方点阵,原子堆积致密,间隙数目少,故间隙半径较大:rA=0.414,R=0.0522nm;r四=0.225,R=0.0284nm
。故上述原子熔入时均处在八面体间隙的中心。如碳在γ-Fe中最大固熔度(质量分数)为WC=2.1l/10-2;氮在γ-Fe中的最大固熔度(质量分数)约为WN=2.8/10-2。5. 密度ρ=5.97g/cm3。6. 两离子的中心距离为0.234nm。7. 碳原子占据10.2%的八面体间隙位置;氮原子占据12.5%的八面体间隙位置。8. 这是因为形成固熔体时,熔质原子的熔入会使熔剂结构产生点阵畸变,从而使体系能量升高。熔质与熔剂原子尺寸相差越大,点阵畸变的程度也越大,则畸变能越高,结构的稳定性越低,熔解度越小。一般来说,间隙固熔体中熔质原子引起的点阵畸变较大,故不能无限互溶,只能有限熔解。9. 9 (1)0.278nm;(2)0.393nm(3)0.482nm;(4)0.622nm;(5)0.393nm。10. (1)WLi+=16/10-2,WMg2+=24/1020,WF-=44/10-2,WO2—=16/10-2(2)该固熔体的密度ρ=2.9g/cm3。 11. 故理论强度介于之间,即4900~7000MPa12. 模子的尺寸l=15.0mm。 13. 故可能是丙酮。14. 画出丁醇(C4H9OH)的4种可能的异构体如下:
15. (1)单体质量为12X2+1X2+35.5X2=97g/mol;(2)聚合度为 n=60000/97=620。16. (1)均方根据长度4.65nm;(2)分子质量m=7125g。17. 理论上的最大应变为3380%。18. 单体的摩尔分数为:X苯烯=20/10-2,X丁二烯=40/10-2,X丙烯晴=40/10-219. (1)和(2)如下:(3)每摩尔的水(0.6X1024)形成时,需要消去0.6X1024的C—O及N—H键,同时形成0.6X1024的C—N及H—O键。净能量变化为-15kJ/mol。 20. 硅酸盐结构的基本特点:(1)硅酸盐的基本结构单元是[Si04]四面体,硅原子位于氧原子四面体的间隙中。硅—氧之间的结合键不仅是纯离子键,还有相当的共价键成分。(2)每一个氧最多只能被两个[Si04]四面体所共有。
(3)[Si04]四面体可以是互相孤立地在结构中存在,也可以通过共顶点互相连接。(4)Si—O--Si的结合键形成一折线。硅酸盐分成下列几类:(1)含有有限硅氧团的硅酸盐;(2)链状硅酸盐;(3)层状硅酸盐;(4)骨架状硅酸盐。 21. 因为大多数陶瓷主要由晶相和玻璃相组成,这两种相的热膨胀系数相差较大,由高温很快冷却时,每种相的收缩不同,所造成的内应力足以使陶瓷器件开裂或破碎。 22. 陶瓷材料中主要的结合键是离子键及共价键。由于离子键及共价键很强,故陶瓷的抗压强度很高,硬度极高。因为原子以离子键和共价键结合时,外层电子处于稳定的结构状态,不能自由运动,故陶瓷材料的熔点很高,抗氧化性好,耐高温,化学稳定性高。 1. 分析结晶相变时系统自由能的变化可知,结晶的热力学条件为∆G<0;由单位体积自由能的变化可知,只有∆T>0,才有∆GB<0。即只有过冷,才能使∆G<0。动力学条件为液—固界面前沿液体的温度T1010℃/s)才能获得玻璃态。为了在较低的冷速下获得金属玻璃,就应增加液态的稳定性,使其能在较宽的温度范围存在。实验证明,当液相线很陡从而有较低共晶温度时,就能增加液态的稳定性,故选用这样的二元系(如Fe—B,Fe—C,h—P,Fe—Si等)。为了改善性能,可以加入一些其他元素(如Ni,Mo,Cr,Co等)。这类金属玻璃可以在10’一10‘℃/s的冷速下获得。9. 实际结晶温度与理论结晶温度之间的温度差,称为过冷度(∆T=Tm一Tn)。它是相变热力学条件所要求的,只有AT>0时,才能造成固相的自由能低于液相自由能的条件,液、固相间的自由能差便是结晶的驱动力。过冷液体中,能够形成等于临界晶核半径的晶胚时的过冷度,称为临界过冷度(∆T*)。显然,当实际过冷度∆T<∆T*时,过冷液体中最大的晶胚尺寸也小于临界晶核半径,故难于成核;只有当∆T>∆T*时,才能均匀形核。所以,临界过冷度是形核时所要求的。
晶核长大时,要求液—固界面前沿液体中有一定的过冷,才能满足(dN/dt)F>(dN/dt)M,这种过冷称为动态过冷度(∆Tk=Tm一Ti),它是晶体长大的必要条件。10. 纯金属生长形态是指晶体宏观长大时界面的形貌。界面形貌取决于界面前沿液体中的温度分布。(1) 平面状长大:当液体具有正温度梯度时,晶体以平直界面方式推移长大。此时,界面上任何偶然的、小的凸起伸入液体时,都会使其过冷度减小,长大速率降低或停止长大,而被周围部分赶上,因而能保持平直界面的推移。长大中晶体沿平行温度梯度的方向生长,或沿散热的反方向生长,而其他方向的生长则受到抑制。(2) 树枝状长大:当液体具有负温度梯度时,在界面上若形成偶然的凸起伸入前沿液体时,由于前方液体有更大的过冷度,有利于晶体长大和凝固潜热的散失,从而形成枝晶的一次轴。一个枝晶的形成,其潜热使邻近液体温度升高,过冷度降低,因此,类似的枝晶只在相邻一定间距的界面上形成,相互平行分布。在一次枝晶处的温度比枝晶间温度要高,如附图2.7(a)中所示的AA断面上丁A>丁n,这种负温度梯度使一次轴上又长出二次轴分枝,如附图2.7(b)所示。同样,还会产生多次分枝。枝晶生长的最后阶段,由于凝固潜热放出,使枝晶周围的液体温度升高至熔点以上,液体中出现正温度梯度,此时晶体长大依靠平界面方式推进,直至枝晶间隙全部被填满为止。11. 根据自由能与晶胚半径的变化关系,可以知道半径rrk的晶胚才有可能成核;而r=rk的晶胚既可能消失,也可能稳定长大。因此,半径为“
的晶胚称为临界晶核。其物理意义是,过冷液体中涌现出来的短程有序的原子团,当其尺寸r≥rk时,这样的原子团便可成为晶核而长大。临界晶核半径rk,其大小与过冷度有关,则有12. 晶体长大机制是指晶体微观长大方式,它与液—固界面结构有关。具有粗糙界面的物质,因界面上约有50%的原子位置空着,这些空位都可接受原子,故液体原子可以单个进入空位,与晶体相连接,界面沿其法线方向垂直推移,呈连续式长大。具有光滑界面的晶体长大,不是单个原子的附着,而是以均匀形核的方式,在晶体学小平面界面上形成一个原子层厚的二维晶核与原界面间形成台阶,单个原子可以在台阶上填充,使二维晶核侧向长大,在该层填满后,则在新的界面上形成新的二维晶核,继续填满,如此反复进行。若晶体的光滑界面存在有螺型位错的露头,则该界面成为螺旋面,并形成永不消失的台阶,原子附着到台阶上使晶体长大。13. 形成单晶体的基本条件是使液体金属结晶时只产生一个核心(或只有一个核心能够长大)并长大成单晶体。14. (1)……在冷却曲线上出现的实际结晶温度与熔点之差……液-固界面前沿液态中的温度与熔点之差。(2)……使体系自由能减小……(3)在过冷液体中,液态金属中出现的……(4)在一定过冷度(>厶了’)下……(5)……就是体系自由能的减少能够补偿2/3表面自由能……(6)……不能成核,即便是有足够的能量起伏提供,还是不能成核。(7)测定某纯金属均匀形核时的有效过冷度……(8)……那么总的形核率N=N2。
(9)……则结晶后就可以形成数万颗晶粒。(10)……非均匀形核的形核功最小。(11)……则只要在工艺上采取对厚处加快冷却(如加冷铁)就可以满足。(12)……因为前者是以外加质点为基底,形核功小……(13)……主要寻找那些熔点高,且……(14)……若液—固界面呈粗糙型,则其液相原子……(15)只有在负温度梯度条件下,常用纯金属……(16)……结晶终了时的组织形态不同,前者呈树枝晶(枝间是水),后者呈一个个(块状)晶粒。(17)……生长过程,但可以通.过实验方法,如把正在结晶的金属剩余液体倒掉,或者整体淬火等进行观察,所以关于树枝状生长形态不是一种推理。(18)……其生长形态不会发生改变。(19)……其界面是粗糙型的。(20)……平直的称为粗糙界面结构……锯齿形的称为平滑界面结构。(21)……因还与液—固界面的结构有关,即与该金属的熔化熵有关。(22)……增加,但因金属的过冷能力小,故不会超过某一极大值……(23)……动态过冷度比形核所需要的临界过冷度小。1. wMg=0.0456。
2. 。3. 设纯溶剂组元A的熔点为TA,液相线与固相线近似为直线,则离界面距离x处液相线温度TL为: 但在x处液相的实际温度T如附图2.8所示,应为:因为溶质分布而产生的成分过冷为:令,得:将(4)代入(3)得:
4. C1合金成分为wMg=0.873,wNi=0.127;C2合金成分为wMg=0.66,wNi=0.3685. (1)高温区水平线为包晶线,包晶反应:Lj+δk→αn 中温区水平线为共晶线,共晶反应:Ld′→αg+βh (2)各区域组织组成物如图4—30中所示。 (3)I合金的冷却曲线和结晶过程如附图2.9所示。 1~2,均匀的液相L。 2~3匀晶转变,L→δ不断结晶出δ相。 3~3′,发生包品反应L+δ→α。 3′~4,剩余液相继续结晶为α。 4,凝固完成,全部为α。 4~5,为单一α相,无变化。 5~6,发生脱溶转变α→βII。室温下的组织为α+βII。
II合金的冷却曲线和结晶过程如附图2.10所示。 1~2,均匀的液相L。 2~3,结晶出α初,随温度下降α相不断析出,液相不断减少。 3~3′,剩余液相发生共晶转变L→α+β。 3′~4,α→βII,β→αII,室温下的组织为。α初+(α+β)共+βII (4)室温时,合金I、II组织组成物的相对量可由杠杆定律求得。 合金I: 合金II:
9. 此说法不正确。固体中的宏观扩散流不是单个原子定向跳动的结果,扩散激活能也不是单个原子迁:移时每一次跳动需越过的能垒,固体中原子的跳动具有随机性质,扩散流是固体中扩散物质质点(如原子,离子)随机跳动的统计结果的宏观体现,当晶体中的扩散以空位机制进行时,晶体中任何一个原子在两个平衡位置之间发生跳动必须同时满足两个条件:(2) 该原子具有的能量必须高于某一临界值∆Gf,即原子跳动激活能,以克服阻碍跳动的阻力;(3) 该原子相邻平衡位置上存在空位。根据统计热力学理论,在给定温度T下,晶体中任一原子的能量高于∆Gf的几率Pf,即晶体中能量高于∆Gf的原子所占原子百分数为而晶体中的平衡空位浓度Cv,即任一原子平衡位置出现空位的几率Pv,为显然,某一瞬间晶体中原子发生一次跳动的几率为P也等于该瞬间发生跳动原子所占的原子百分数。其中Q=∆Gf+∆Gv,就是空位扩散机制的扩散激活能。11. 因α-Fe中的最大碳熔解度(质量分数)只有0.0218%,对于含碳质量分数大于0.0218%的钢铁在渗碳时零件中的碳浓度梯度为零,渗碳无法进行,即使是纯铁,在α相区渗碳时铁中浓度梯度很小,在表也不能获得高含碳层;另外,由于温度低,扩散系数也很小,渗碳过程极慢,没有实际意义。γ-Fe中的碳固溶度高,渗碳时在表层可获得较高的碳浓度梯度使渗碳顺利进行。
12. 原因是。α-Fe中的扩散系数较γ-Fe中的扩散系数高。13. 转折点向低温方向移动。14. 三元系扩散层内不可能存在三相共存区,但可以存在两相共存区。原因如下:三元系中若出现三相平衡共存,其二相中成分一定且不同相中同一组分的化学位相等,化学位梯度为零,扩散不可能发生。三元系在两相共存时,由于自由度数为2,在温度一定时,其组成相的成分可以发生变化,使两相中相同组元的原子化学位平衡受到破坏,引起扩散。15. (1)固体中即使不存在宏观扩散流,但由于原子热振动的迁移跳跃,扩散仍然存在。纯物质中的自扩散即是一个典型例证。(2) 原子每次跳动方向是随机的。只有当系统处于热平衡状态,原子在任一跳动方向上的跳动几率才是相等的。此时虽存在原子的迁移(即扩散),但没有宏观扩散流。如果系统处于非平衡状态,系统中必然存在热力学势的梯度(具体可表示为浓度梯度、化学位梯度、应变能梯度等)。原子在热力学势减少的方向上的跳动几率将大于在热力学势增大方向上的跳动几率。于是就出现了宏观扩散流。(3) 晶界上原子排列混乱,与非晶体相类似,其原子堆积密集程度远不及晶粒内部,因而对原子的约束能力较弱,晶界原子的能量及振动频率ν明显高于晶内原子。所以晶界处原子具有更高的迁移能力。晶界扩散系数也罢明显鬲于晶内扩散系数。(4) 事实上这种情况不可能出现。间隙固熔体的熔质原子固熔度十分有限。即使是达到过饱合状态,溶质原子数目要比晶体中的间隙总数要小几个数量级,因此,在间隙原子周围的间隙位置可看成都是空的。即对于给定晶体结构,z为一个常数。(5) 虽然体心立方晶体的配位数小,但其属于非密堆结构。与密堆结构的面心立方晶体相比较,公式中的相关系数f值相差不大(0.72和0.78),但原子间距大,原子因约束力小而振动频率ν高,其作用远大于配位数的影响。而且原子迁移所要克服的阻力也小,具体表现为扩散激活能低,扩散常数较大,实际情况是在同一温度下α-Fe有更高的自扩散系数,而且熔质原子在。α-Fe中的扩散系数要比γ-Fe高。
1. (1)临界分切应力n及取向因子数据如附表2.3所示。 以上数据表明,实验结果符合临界分切应力定律τk=σm。(2)屈服应力σs与取向因子,m之间的关系如附图2.17所示。6. 单滑移是指只有一个滑移系进行滑移。滑移线呈一系列彼此平行的直线。这是因为单滑移仅有一组多滑移是指有两组或两组以上的不同滑移系同时或交替地进行滑移。它们的滑移线或者平行,或者相交成一定角度。这是因为一定的晶体结构中具有一定的滑移系,而这些滑移系的滑移面之间及滑移方向之间都交滑移是指两个或两个以上的滑移面沿共同的滑移方向同时或交替地滑移。它们的滑移线通常为折线或波纹状。只是螺位错在不同的滑移面上反复“扩展”的结果。10. 滑移带一般不穿越晶界。如果没有多滑移时,以平行直线和波纹线出现,如附图2.19(a),它可以通过抛光而去除。机械孪晶也在晶粒内,因为它在滑移难以进行时发生,而当孪生使晶体转动后,又可使晶体滑移。所以一般孪晶区域不大,如附图2.19(b)所示。孪晶与基体位向不同,不能通过抛光去除。退火孪晶以大条块形态分布于晶内,孪晶界面平直,一般在金相磨面上分布比较均匀,如附图2。19(c)所示,且不能通过抛光去除。11. 低碳钢的屈服现象可用位错理论说明。由于低碳钢是以铁素体为基的合金,铁素体中的碳(氮)原子与位错交互作用,总是趋于聚集在位错线受拉应力的部位以降低体系的畸变能,形成柯氏气团对位错起“钉扎”作用,致使σs升高。而位错一旦挣脱气团的钉扎,便可在较小的应力下继续运动,这时拉伸曲线上又会出现下屈服点。已经屈服的试样,卸载后立即重新加载拉伸时,由于位错已脱出气团的钉扎,故不出现屈服点。但若卸载后,放置较长时间或稍经加热后,再进行拉伸时,由于熔质原子已通过热扩散又重新聚集到位错线周围形成气团,故屈服现象又会重新出现。吕德斯带会使低碳薄钢板在冲压成型时使工件表面粗糙不平。其解决办法,可根据应变时效原理,将钢板在冲压之前先进行一道微量冷轧(如1%~2%的压下量)工序,使屈服点消除,随后进行冲压成型,也可向钢中加入少量Ti,A1及C,N等形成化合物,以消除屈服点。
12. 材料经冷加工后,除使紊乱取向的多晶材料变成有择优取向的材料外,还使材料中的不熔杂质、第二相和各种缺陷发生变形。由于晶粒、杂质、第二相、缺陷等都沿着金属的主变形方向被拉长成纤维状,故称为纤维组织。一般来说,纤维组织使金属纵向(纤维方向)强度高于横向强度。这是因为在横断面上杂质、第二相、缺陷等脆性、低强度“组元”的截面面积小,而在纵断面上截面面积大。当零件承受较大载荷或承受冲击和交变载荷时,这种各向异性就可能引起很大的危险。金属在冷加工以后,各晶粒的位向就有一定的关系。如某些晶面或晶向彼此平行,且都平行于零件的某一外部参考方向,这样一种位向分布就称为择优取向或简称为织构。形成织构的原因并不限于冷加工,而这里主要是指形变织构。无论从位向还是从性能看,有织构的多晶材料都介于单晶体和完全紊乱取向的多晶体之间。由于织构引起金属各向异性,在很多情况下给金属加工带来不便,如冷轧镁板会产生(0001)<1120>织构,若进一步加工很容易开裂;深冲金属杯的制耳,金属的热循环生长等。但有些情况下也有其有利的一面。13. 加工硬化是由于位错塞积、缠结及其相互作用,阻止了位错的进一步运动,流变应力。细晶强化是由于晶界上的原子排列不规则,且杂质和缺陷多,能量较高,阻碍位错的通过,;且晶粒细小时,变形均匀,应力集中小,裂纹不易萌生和传播。固熔强化是由于位错与熔质原子交互作用,即柯氏气团阻碍位错运动。弥散强化是由于位错绕过、切过第二相粒子,需要增加额外的能量(如表面能或错排能);同时,粒子周围的弹性应力场与位错产生交互作用,阻碍位错运动。14. 气泡阻碍位错运动的机制是由于位错通过气泡时,切割气泡,增加了气泡—金属间界面的面积,因此需要增加外切应力做功,即提高了金属钨的强度。
设位错的柏氏矢量为b,气泡半径为r,则位错切割气泡后增加的气泡—金属间界面面积为A=2rb。设气泡—金属的比界面能为σ,则界面能增值为2rbσ。若位错切割一个气泡的切应力增值为∆τ’,,则应力所做功为∆τ’b。所以2rbσ=∆τ’b,即:2rσ=∆τ’当气泡密度为n时,则切应力总增值:∆τ=n∆τ’=2nrσ可见,切应力增值与气泡密度成正比。15. 作为一类材料,陶瓷是比较脆的。晶态陶瓷缺乏塑性是由于其离子键和共价键造成的。在共价键键合的陶瓷中,原子之间的键合是特定的并具有方向性,如附图2.20(a)所示。当位错以水平方向运动时,必须破坏这种特殊的原子键合,而共价键的结合力是很强的,位错运动有很高的点阵阻力(即派—纳力)。因此,以共价键键合的陶瓷,不论是单晶体还是多晶体,都是脆的。基本上是离子键键合的陶瓷,它的变形就不一样。具有离子键的单晶体,如氧化铁和氯化钠,在室温受压应力作用时可以进行相当多的塑性变形,但是具有离子键的多晶陶瓷则是脆的,并在晶界形成裂纹。这是因为可以进行变形的离子晶体,如附图2.20(b)所示,当位错运动一个原子间距时,同号离子的巨大斥力,使位错难以运动;但位错如果沿45°方向而不是水平方向运动,则在滑移过程中相邻晶面始终由库仑力保持相吸,因而具有相当好的塑性。但是多晶陶瓷变形时,相邻晶粒必须协调地改变形状,由于滑移系统较少而难以实现,结果在晶界产生开裂,最终导致脆性断裂。16. 这是由于陶瓷粉末烧结时存在难以避免的显微空隙。在冷却或热循环时由热应力产生了显微裂纹,由于腐蚀所造成的表面裂纹,使得陶瓷晶体与金属不同,具有先天性微裂纹。在裂纹尖端,会产生严重的应力集中,按照弹性力学估算,裂纹尖端的最大应力已达到理论断裂强度或理论屈服强度(因为陶瓷晶体中可动位错很少,而位错运动又很困难,故一旦达到屈服强度就断裂了)。反过来,也可以计算当裂纹尖端的最大应力等于理论屈服强度时,晶体断裂的名义应力,它和实际得出的抗拉强度极为接近。陶瓷的压缩强度一般为抗拉强度的15
倍左右。这是因为在拉伸时当裂纹一达到临界尺寸就失稳扩展而断裂;而压缩时裂纹或者闭合或者呈稳态地缓慢扩展,并转向平行于压缩轴。即在拉伸时,陶瓷的抗拉强度是由晶体中的最大裂纹尺寸决定的,而压缩强度是由裂纹的平均尺寸决定的。18. 玻璃态高聚物在Tb~Tg之间或部分结晶高聚物在Tg~Tm之间的典型拉伸应力—应变曲线表明,过了屈服点之后,材料开始在局部地区(如应力集中处)出现颈缩,再继续变形时,其变形不是集中在原颈缩处,使得该处愈拉愈细,而是颈缩区扩大,不断沿着试样长度方向延伸,直到整个试样的截面尺寸都均匀减小。在这一段变形过程中应力几乎不变,如附图2.21所示。在开始出现颈缩后,继续变形时颈缩沿整个试样扩大,这说明原颈缩处出现了加工硬化。X射线证明,高聚物中的大分子无论是呈无定形态还是呈结晶态,随着变形程度的增加,都逐渐发生了沿外力方向的定向排列。由于键的方向性(主要是共价键)在产生定向排列之后,产生了应变硬化。把已冷拉高聚物的试样加热到Tg以上,形变基本上全能回复。这说明非晶态高聚物冷拉中产生的形变属高弹性形变范畴。部分结晶高聚物冷拉后残留的形变中大部分必须升温至丁-附近时才能回复。这是因为部分结晶高聚物的冷拉中伴随着晶片的排列与取向,而取向的晶片在Tm以下是热力学稳定的。19.银纹不同于裂纹。裂纹的两个张开面之间完全是空的,而银纹面之间由高度取向的纤维束和空穴组成,仍具有一定的强度。银纹的形成是由于材料在张应力作用下局部屈服和冷拉造成。祝愿同学们可以考上西工大。。。。。。。。。。。。。。20.1. 可用金相法求再结晶形核率N和长大线速度G。具体操作:
(1) 测定N:把一批经大变形量变形后的试样加热到一定温度(丁)后保温,每隔一定时间t,取出一个试样淬火,把做成的金相样品在显微镜下观察,数得再结晶核心的个数N,得到一组数据(数个)后作N—t图,在N—t曲线上每点的斜率便为此材料在温度丁下保温不同时间时的再结晶形核率N。(2) 测定G:将(1)中淬火后的一组试样进行金相观察,量每个试样(代表不同保温时间)中最大晶核的线尺寸D,作D—t图,在D—t曲线上每点的斜率便为了温度下保温不同时间时的长大线速度G。2. 再结晶退火必须用于经冷塑性变形加工的材料,其目的是改善冷变形后材料的组织和性能。再结晶退火的温度较低,一般都在临界点以下。若对铸件采用再结晶退火,其组织不会发生相变,也没有形成新晶核的驱动力(如冷变形储存能等),所以不会形成新晶粒,也就不能细化晶粒。3. 能。可经过冷变形而后进行再结晶退火的方法。4. 答案如附表2.5所示。附表2.5 冷变形金属加热时晶体缺陷的行为缺陷表现、物理变化晶体缺陷的行为缺陷运动驱动力 冷加工变形时主要的形变方式是滑移,由于滑移,晶体中空位和位错密度增加,位错分布不均匀切应力作用回复空位扩散、集聚或消失;位错密度降低,位错相互作用重新分布(多边化)弹性畸变能再结晶毗邻低位错密度区晶界向高位错密度的晶粒扩张。位错密度减少,能量降低,成为低畸变或无畸变区形变储存能晶粒长大弯曲界面向其曲率中心方向移动。微量杂质原子偏聚在晶界区域,对晶界移动起拖曳作用。这与杂质吸附在位错中组成柯氏气团阻碍位错运动相似,影响了晶界的活动性晶粒长大前后总的界面能差,而界面移动的驱动力是界面曲率5. (1)铜片经完全再结晶后晶粒大小沿片长方向变化示意图如附图2.22
所示。由于铜片宽度不同,退火后晶粒大小也不同。最窄的一端基本无变形,退火后仍保持原始晶粒尺寸;在较宽处,处于临界变形范围,再结晶后晶粒粗大;随宽度增大,变形度增大,退火后晶粒变细,最后达到稳定值。在最宽处,变形量很大,在局部地区形成变形织构,退火后形成异常大晶粒。(2)变形越大,冷变形储存能越高,越容易再结晶。因此,在较低温度退火,在较宽处先发生再结晶。6. 再结晶终了的晶粒尺寸是指再结晶刚完成但未发生长大时的晶粒尺寸。若以再结晶晶粒中心点之间的平均距离d表征再结晶的晶粒大小,则d与再结晶形核率N及长大线速度之间有如下近似关系:且由于Qn与Qg几乎相等,故退火温度对G/N比值的影响微弱,即晶粒大小是退火温度的弱函数。故图中曲线中再结晶终了的晶粒尺寸与退火温度关系不大。再结晶完成以后,若继续保温,会发生晶粒长大的过程。对这一过程而言,退火温度越高,(保温时间相同时)退火后晶粒越大。这是因为晶粒长大过程是通过大角度晶界的移动来进行的。温度越高,晶界移动的激活能就越低,晶界平均迁移率就越高,晶粒长大速率就越快,在相同保温时间下,退火后的晶粒越粗大,这与前段的分析并不矛盾。8. 前种工艺,由于铝件变形处于临界变形度下,故退火时可形成个别再结晶核心,最终晶粒极为粗大,而后种工艺,是由于进行再结晶退火时的温度选择不合理(温度过高),若按T再=0.4T熔估算,则T再=100℃,故再结晶温度不超过200℃为宜。由于采用630℃退火1h,故晶粒仍然粗大。综上分析,在80%变形量条件下,采用150℃退火1h,则可使其晶粒细化。9. 前者采用去应力退火(低温退火);后者采用再结晶退火(高温退火)。10. 去应力退火过程中,位错通过攀移和滑移重新排列,从高能态转变为低能态;动态回复过程中,则是通过螺位错的交滑移和刃位错的攀移,使异号位错相互抵消,保持位错增殖率与位错消失率之间的动态平衡。
从显微组织上观察,静态回复时可见到清晰的亚晶界,静态再结晶时形成等轴晶粒;而动态回复时形成胞状亚结构,动态再结晶时等轴晶中又形成位错缠结胞,比静态再结晶晶粒要细。11. 一是不在两相区变形;二是减少夹杂元素含量;三是采用高温扩散退火,消除元素偏析。对已出现带状组织的材料,在单相区加热、正火处理,则可予以消除或改善。12. 金属材料在热加工过程中经历了动态变形和动态回复及再结晶过程,柱状晶区和粗等轴晶区消失了,代之以较细小的等轴晶粒;原铸锭中许多分散缩孔、微裂纹等由于机械焊合作用而消失,显微偏析也由于压缩和扩散得到一定程度的减弱,故使材料的致密性和力学性能(特别是塑性、韧性)提高。13. 可以在钨丝中形成弥散、颗粒状的第二相(如ThO2)以限制晶粒长大。因为若ThO2的体积分数为φ,半径为r时,晶粒的极限尺寸 (α为接触角);若选择合适的φ和r,使R尽可能小,即晶粒不再长大。由于晶粒细化将使灯丝脆性大大下降而不易破断,从而有效地延长其寿命。15.(1)不对。对于冷变形(较大变形量)后的金属,才能通过适当的再结晶退火细化晶粒。(2) 不对。有些金属的再结晶温度低于室温,因此在室温下的变形也是热变形,也会发生动态再结晶。(3) 不对。多边化过程中,空位浓度下降、位错重新组合,致使异号位错互相抵消,位错密度下降,使点阵畸变减轻。(4) 不对。如果在临界变形度下变形的金属,再结晶退火后,晶粒反而粗化。(5) 不对。再结晶不是相变。因此,它可以在一个较宽的温度范围内变化。(6) 不对。微量熔质原子的存在(20#钢中WC=0.002),会阻碍金属的再结晶,从而提高其再结晶温度。(7) 不对。只有再结晶过程才是形核及核长大过程,其驱动力是储存能。
(8) 不对。金属的冷变形度较小时,相邻晶粒中才易于出现变形不均匀的情况,即位错密度不同,越容易出现晶界弓出形核机制。(9) 不对。晶粒正常长大,是在界面曲率作用下发生的均匀长大;反常长大才是大晶粒吞食小晶粒的不均匀长大。(10) 不对。合金中的第二相粒子一般可阻碍再结晶,也会阻止晶粒长大。(11) 不对。再结晶织构是冷变形金属在再结晶(一次,二次)过程中形成的织构。它是在形变织构的基础上形成的,有两种情况,一是保持原有形变织构,二是原有形变织构消失,而代之以新的再结晶织构。(12) 不对。正常晶粒长大是在再结晶完成后继续加热或保温过程中,晶粒发生均匀长大的过程,而反常晶粒长大是在一定条件下(即再结晶后的晶粒稳定、存在少数有利长大的晶粒和高温加热),继晶粒正常长大后发生的晶粒不均匀长大过程。(13) 不对。再结晶虽然是形核—长大过程,但晶体点阵类型并未改变,故不是相变过程。祝愿同学们可以考上西工大。。。。。。。。。。。。。。1. 固态相变时形核的阻力,来自新相晶核与基体间形成界面所增加的界面能Eγ,以及体积应变能(即弹性能)Ee。其中,界面能Eγ包括两部分:一部分是在母相中形成新相界面时,由同类键、异类键的强度和数量变化引起的化学能,称为界面能中的化学项;另一部分是由界面原子不匹配(失配),原子间距发生应变引起的界面应变能,称为界面能中的几何项。应变能Ee
产生的原因是,在母相中产生新相时,由于两者的比体积不同,会引起体积应变,这种体积应变通常是通过新相与母相的弹性应变来调节,结果产生体积应变能。从总体上说,随着新相晶核尺寸的增加及新相的生长,(Eγ+Ee)会增加。当然,Eγ、Ee也会通过新相的析出位置、颗粒形状、界面状态等,相互调整,以使(Eγ+Ee)为最小。母相为液态时,不存在体积应变能问题;而且固相界面能比液—固的界面能要大得多。相比之下,固态相变的阻力大。2. 如同在液相中一样,固相中的形核几乎总是非均匀的,这是由于固相中的非平衡缺陷(诸如非平衡空位、位错、晶界、层错、夹杂物等)提高了材料的自由能。如果晶核的产生结果使缺陷消失,就会释放出一定的自由能,因此减少了激活能势垒。新相在位错处形核有三种情况:一是新相在位错线上形核,新相形成处,位错消失,释放的弹性应变能量使形核功降低而促进形核;二是位错不消失,而且依附在新相界面上,成为半共格界面中的位错部分,补偿了失配,因而降低了能量,使生成晶核时所消耗的能量减少而促进形核;三是当新相与母相成分不同时,由于溶质原子在位错线上偏聚(形成柯氏气团)有利于新相沉淀析出,也对形核起促进作用。4. 脱溶顺序为:T1温度,α-θ’-θ;T2温度,α-θ”-θ’-θ。判断一个新相能否形成,除了具有负的体积自由能外,还必须考虑新相形成时的界面能和应变能。由临界形核功可知,只有当界面能γα/β和应变能Es
,尽可能减小,才能有效地减小临界形核功,有利于新相形核。在析出初期阶段,析出相很细小,此时应变能较小,而表面能很大。为了减小表面能,新相往往形成与母相晶格接近,并与母相保持共格的亚稳过渡相,以使体系能量降低,有利于相变。在析出后期,由于析出相粒子长大,应变能上升为相变的主要阻力,则新相形成与母相非共格的稳定相,以降低体系总能量。随时效温度不同,由于界面能和应变能的不同作用,将出现不同的亚稳过渡相。6. 如果脱熔是在母相中各处同时发生,且随新相的形成母相成分发生连续变化,但其晶粒外形及位向均不改变,称之为连续脱熔。与连续脱熔相反,当脱熔一旦发生,其周围一定范围内的固熔体立即由过饱和状态变成饱和状态,并与母相原始成分形成明显界面。在晶界形核后,以层片相间分布并向晶内生长。通过界面不但发生成分突变,且取向也发生了改变,这就是不连续脱熔。其主要差别在于扩散途径的长度。前者扩散场延伸到一个相当长的距离,而后者扩散距离只是片层间距的数量级(一般小于1mm)不连续脱熔有以下特征:(1) 在析出物与基体界面上,成分是不连续的;析出物与基体间的界面都为大角度的非共格界面,说明晶体位向也是不连续的。(2) 胞状析出物通常在基体(α’)晶界上形核,而且总是向。’相的相邻晶粒之一中长大。(3) 胞状析出物长大时,熔质原子的分配是通过其在析出相与母相之间的界面扩散来实现的,扩散距离通常小于1mm。6. A1—Cu合金的脱溶系列有:GP区-θ"过渡相-θ’过渡相-θ平衡相脱熔相的基本特征:GP区为圆盘状,其厚度为0.3~0.6nm,直径约为8nm,在母相的{100}面上形成。点阵与基体α相同(fcc),并与α相完全共格。θ"过渡相呈圆片状,其厚度为2nm,直径为30~40nm,在母相的{100}面上形成。具有正方点阵,点阵常数为a=b=0.404nm,c=0.78nm,与基体完全共格,但在z轴方向因点阵常数不同而产生约4%的错配,故在θ"附近形成一个弹性共格应变场。
θ"过渡相也在基体的{100}面上形成,具有正方结构,点阵常数a=b=0.404nm,c=0.58nm,其名义成分为CuAl2。由于在z轴方向错配量太大,所以只能与基体保持局部共格。θ相具有正方结构,点阵常数a=b=0.607nm,c=0.487nm,这种平衡沉淀相与基体完全失去共格。时效的实质,就是从过饱和固熔体分离出一个新相的过程,通常这个过程是由温度变化引起的。时效以后的组织中含有基体和沉淀物,基体与母相的晶体结构相同,但成分及点阵常数不同;而沉淀物则可以具有与母相不同的晶体结构和成分。由于沉淀物的性质、大小、形状及在显微组织中的分布不同,合金的性能可以有很大的变化。7. 调幅分解是指过饱和固熔体在一定温度下分解成结构相同、成分和点阵常数不同的两个相。调幅分解的主要特征是不需要形核过程。调幅分解与形核、长大脱熔方式的比较如附表2.6所示。 调幅分解与形核、长大脱熔方式的比较脱熔类型自由能成分曲线特点条 件形核特点界面特点扩散方式转变速率颗粒大小调幅分解凸自发涨落非形核宽泛上坡高数量多、颗粒小形核长大凹过冷度及临界形核功形核明晰下坡低颗粒大、数量少8. 若固态合金中,含有大小不同的沉淀相粒子,在高温退火时,将会出现小粒子熔解,大粒子长大的现象。其物理实质:假定始态只有附图2.23(a)所示的两种尺寸的第二相粒子。由粒子大小对固熔度的影响可知,小粒子的固熔度较大,因而在。相内,从小粒子到大粒子之间,有一个从高到低的熔质浓度梯度,小粒子周围的熔质有向大粒子周围扩散的趋势。这种扩散发生后,破坏了亚稳平衡,使小粒子周围的熔质浓度(Cr2)小于亚稳平衡时的熔质浓度(Cr1),如附图2.23(b)所示,因而小粒子熔解而变得更小,如附图2.23(c)所示;而大粒子周围的熔质浓度(Cr2’)又大于亚稳平衡时的熔质浓度(Cr1’),因而发生沉淀,使大粒子长大,如附图2.23(c)所示。因此,不均匀尺寸的固相粒子粗化,是通过小粒子继续熔解以及大粒子继续长大而进行的。
9. 直径2r=6×10-6m。10. 无扩散型相变具有如下特点:(1) 存在由于均匀切变引起的形状改变,使晶体发生外形变化。(2) 由于相变过程无扩散,新相与母相的化学成分相同。(3) 母相与新相之间有一定的晶体学位向关系。(4) 相界面移动速度极快,可接近声速。13. 860℃加热,两种钢均在单相区(见Fe—Fe3C相图),淬火后均为M体。WC=0.012的碳钢中有一定量的残余奥氏体。WC=0.003的碳钢,其马氏体成分为WC=0.003,形态为板条状,精细结构为位错。WC=0.012的碳钢,其马氏体成分为WC=0.012,形态为针状,精细结构为孪晶。WC=0.003的碳钢,在200℃以下回火时,组织形态变化较小,硬度变化也不大。但碳原子向位错线附近偏聚倾向增大。当回火温度高于250℃时,渗碳体在板条间或沿位错线析出,使强度、塑性降低;当回火温度达300~400℃时,析出片状或条状渗碳体,硬度、强度显著降低,塑性开始增高,当400~700℃回火时,发生碳化物的聚集、长大和球化及。相的回复、再结晶。此时,硬度、强度逐渐降低,塑性逐渐增高。WC=0.012的碳钢,低于100℃回火时,碳原子形成富碳区;100~200℃回火时,析出大量细小碳化物,因此,硬度稍有提高;200~300℃回火时,残留奥氏体转变为回火马氏体(或贝氏体)使硬度升高,但同时,马氏体的硬度降低,因此,总体上硬度变化不大;高于300℃回火时,碳化物继续析出,随后便是碳化物长大及球化,而α相发生回复、再结晶,使硬度降低,韧性增高。祝愿同学们可以考上西工大。。。。。。。。。。。。。。
1. 体主要用于固定和粘附增强体,并将所受的载荷通过界面传递到增强体上,当然自身也承受少量载荷。基体是能起到类似隔膜的作用,将增强体分隔开来,当有的增强体发生损伤和断裂时,裂纹不致从一个增强体传播到另一个增强体。在复合材料的加工和使用中,基体还能保护增强体免受环境的化学作用和物理损伤等。从增强体在结构复合材料中主要承担载荷角度看,通常要求增强体具有高强度和高模量,增强体的体积分数,与基体的结合性能对复合材料的性能起着很大的影响。增强体,基体和界面共同作用,可以改变复合材料的韧性、抗疲劳性能、抗蠕变性能、抗冲击性能及其他性能。界面能起到协调基体和增强体变形的作用,通过界面可将基体的应力传递到增强体上,基体和增强体通过界面发生结合,但结合力的大小要适当,既不能过大,也不能太小,结合力过大会使复合材料韧性下降,结合力过小,起不到传递应力的作用,容易在界面处开裂。3. 弥散增强:主要针对金属基体,加入硬质颗粒如A12O3,,TiC,SiC等,其粒径为0.01~0.1mm左右,这些弥散于金属或合金中的颗粒,可以有效的阻止位错的运动,起到显著的强化作用,但基体仍是承受载荷的主体。粒子增强:在基体中加入直径为1~50mm的硬质颗粒,粒子可承担部分载荷。但基体承担主要载荷。微粒以机械约束的方式限制基体变形。粒径适当搭配并均匀分布,从而起到有效的强化。纤维增强:①连续纤维增强可用混合定则来解释,载荷和模量主要由纤维起作用。由于纤维强度和模量远高于墓体,并大于纤维临界体积分数,故起到增强作用,界面结合要适中。②短纤维和晶须增强复合材料中纤维长度应大于临界长度,或长径比应大于临界值。纤维是强度和模量的主要贡献者,由于纤维强度和模量远高于基体,界面结合要适中。
4. (1)从复合材料结构单元和尺度上讲,把增强颗粒尺度为1~50mm的叫颗粒增强复合材料,把0.1mm尺度增强叫弥散强化复合材料,而把亚微米至纳米级叫精细复合材料,其强化原理各不相同。(2)纤维破坏概率F(σ)=1-exp(-αlσβ)和纤维平均强度;σ=(αl)-1/βG(1+1/β)都与纤维的长度l有关。纤维增强的复合材料的性能不仅与纤维的长度有关,与纤维的长径比l/d也有关,还与复合材料板的厚度有关。这些都是复合材料尺寸效应的体现。(3)复合材料试样越大,含缺陷概率越高,强度越低。5. 临界体积分数的意义:纤维体积分数大于临界体积分数时,复合材料强度高于基体强度。纤维体积分数小于临界体积分数时,复合材料强度小于基体强度,起不到增强作用。6. 按照短纤维复合材料中的剪滞理论,纤维中的最大应力为,亦即纤维中的最大应力和纤维长度l成线性关系。LC对应与纤维中最大应力(σf)max等于纤维断裂应力σfu。所以当L
您可能关注的文档
- 100分的选择:尔雅《美学原理》作业考试.docx
- 11年天津市事业单位《职业能力测验》真题及答案.doc
- 1203春东财《施工企业会计》在线作业一二三习题及答案.docx
- 12财管习题答案完整版.doc
- 14年上海财经大学上财801803经济学考研资料真题答案笔记.doc
- 1999-2009年初级会计职称考试《初级会计实务》试题及答案.pdf
- 1《建筑施工技术》试题及答案.doc
- 1曼昆经济学原理_课后答案.docx.doc
- 1机械设计(第八版)课后习题答案(最新).doc
- 2000年临床执业医师《医学综合(笔试部分)4》试题及答案.doc
- 2001年4月到2012年4月自学考试《国际经济法概论》历年真题及部分答案.doc
- 2001年临床执业医师《医学综合(笔试部分)3》试题及答案.doc
- 2002-2014年4月高等教育自学考试《金融理论与实务》试题及答案.docx
- 2003-2013年中级会计职称考试《经济法》试题及答案.doc
- 2003-2014年中级《中级会计实务》试题及答案.doc
- 2003-2014年中级《财务管理》试题及答案.doc
- 2003-2015全国职称英语等级考试卫生类A级历年真题及答案.doc
- 2003-2015年广东省小学《育苗杯》初复赛试题及答案.doc