[工程流体力学(水力学)] 禹华谦1-5章习题解答

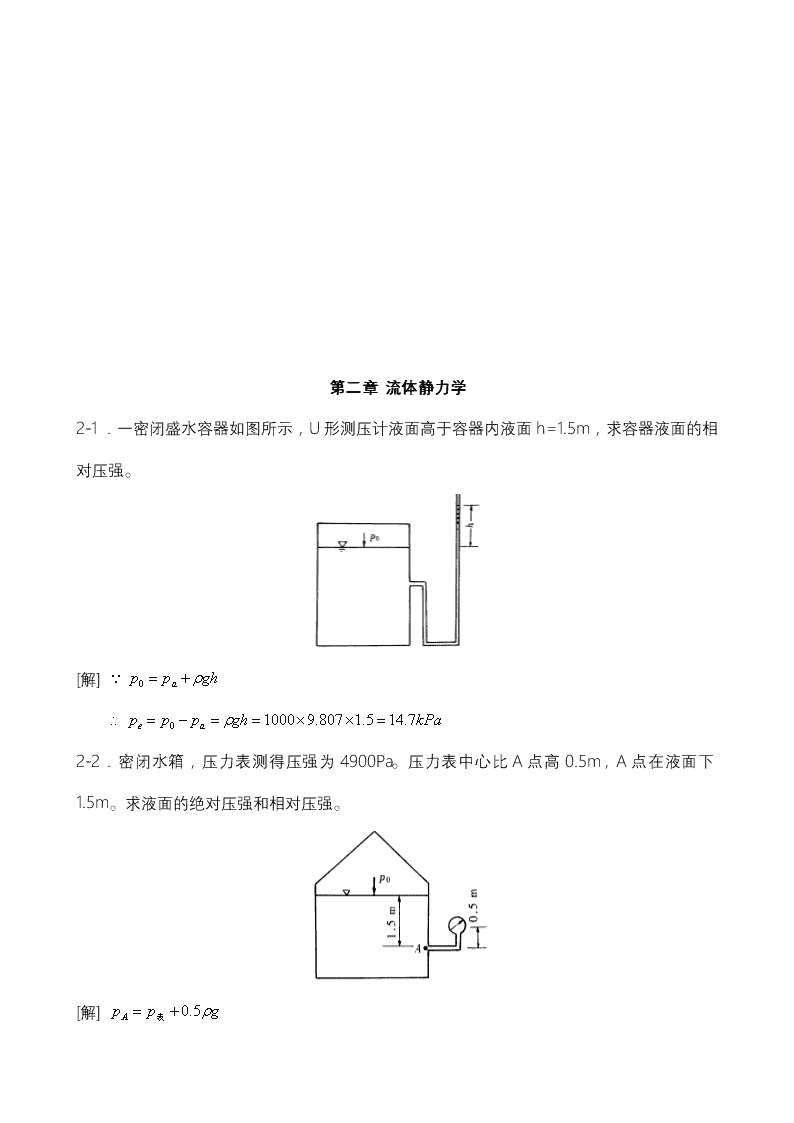
'第一章绪论1-1．20℃的水2.5m3，当温度升至80℃时，其体积增加多少？[解]温度变化前后质量守恒，即又20℃时，水的密度80℃时，水的密度则增加的体积为1-2．当空气温度从0℃增加至20℃时，运动粘度增加15%，重度减少10%，问此时动力粘度增加多少（百分数）？[解]此时动力粘度增加了3.5%1-3．有一矩形断面的宽渠道，其水流速度分布为，式中、分别为水的密度和动力粘度，为水深。试求时渠底（y=0）处的切应力。[解]当=0.5m，y=0时1-4．一底面积为45×50cm2，高为1cm的木块，质量为5kg ，沿涂有润滑油的斜面向下作等速运动，木块运动速度u=1m/s，油层厚1cm，斜坡角22.620（见图示），求油的粘度。[解]木块重量沿斜坡分力F与切力T平衡时，等速下滑1-5．已知液体中流速沿y方向分布如图示三种情况，试根据牛顿内摩擦定律，定性绘出切应力沿y方向的分布图。[解] 第二章流体静力学2-1．一密闭盛水容器如图所示，U形测压计液面高于容器内液面h=1.5m，求容器液面的相对压强。[解]2-2．密闭水箱，压力表测得压强为4900Pa。压力表中心比A点高0.5m，A点在液面下1.5m。求液面的绝对压强和相对压强。[解] 2-3．多管水银测压计用来测水箱中的表面压强。图中高程的单位为m。试求水面的绝对压强pabs。[解]2-4．水管A、B两点高差h1=0.2m，U形压差计中水银液面高差h2=0.2m。试求A、B两点的压强差。（22.736N／m2）[解]2-5．水车的水箱长3m,高1.8m，盛水深1.2m，以等加速度向前平驶，为使水不溢出，加速度a的允许值是多少？ [解]坐标原点取在液面中心，则自由液面方程为：当时，，此时水不溢出2-6．矩形平板闸门AB一侧挡水。已知长l=2m，宽b=1m，形心点水深hc=2m，倾角=45，闸门上缘A处设有转轴，忽略闸门自重及门轴摩擦力。试求开启闸门所需拉力。[解]作用在闸门上的总压力：作用点位置：2-7．图示绕铰链O转动的倾角=60°的自动开启式矩形闸门，当闸门左侧水深h1=2m ，右侧水深h2=0.4m时，闸门自动开启，试求铰链至水闸下端的距离x。[解]左侧水作用于闸门的压力：右侧水作用于闸门的压力：2-8．一扇形闸门如图所示，宽度b=1.0m，圆心角=45°，闸门挡水深h=3m，试求水对闸门的作用力及方向[解]水平分力：压力体体积： 铅垂分力：合力：方向：2-9．如图所示容器，上层为空气，中层为的石油，下层为的甘油，试求：当测压管中的甘油表面高程为9.14m时压力表的读数。[解]设甘油密度为，石油密度为，做等压面1--1，则有2-10．某处设置安全闸门如图所示，闸门宽b=0.6m，高h1=1m，铰接装置于距离底h2=0.4m，闸门可绕A点转动，求闸门自动打开的水深h为多少米。[解]当时，闸门自动开启将代入上述不等式 得2-11．有一盛水的开口容器以的加速度3.6m/s2沿与水平面成30o夹角的斜面向上运动，试求容器中水面的倾角。[解]由液体平衡微分方程，，在液面上为大气压，2-12．如图所示盛水U形管，静止时，两支管水面距离管口均为h，当U形管绕OZ轴以等角速度ω旋转时，求保持液体不溢出管口的最大角速度ωmax。[解]由液体质量守恒知，I管液体上升高度与II管液体下降高度应相等，且两者液面同在一等压面上，满足等压面方程：液体不溢出，要求，以分别代入等压面方程得： 2-13．如图，，上部油深h1＝1.0m，下部水深h2＝2.0m，油的重度=8.0kN/m3，求：平板ab单位宽度上的流体静压力及其作用点。[解]合力作用点：2-14．平面闸门AB倾斜放置，已知α＝45°，门宽b＝1m，水深H1＝3m，H2＝2m，求闸门所受水静压力的大小及作用点。 [解]闸门左侧水压力：作用点：闸门右侧水压力：作用点：总压力大小：对B点取矩：2-15．如图所示，一个有盖的圆柱形容器，底半径R＝2m，容器内充满水，顶盖上距中心为r0处开一个小孔通大气。容器绕其主轴作等角速度旋转。试问当r0多少时，顶盖所受的水的总压力为零。 [解]液体作等加速度旋转时，压强分布为积分常数C由边界条件确定：设坐标原点放在顶盖的中心，则当时，（大气压），于是，在顶盖下表面，，此时压强为顶盖下表面受到的液体压强是p，上表面受到的是大气压强是pa，总的压力为零，即积分上式，得，2-16．已知曲面AB为半圆柱面，宽度为1m，D=3m，试求AB柱面所受静水压力的水平分力Px和竖直分力Pz。[解]水平方向压强分布图和压力体如图所示： 2-17．图示一矩形闸门，已知及，求证>时，闸门可自动打开。[证明]形心坐标则压力中心的坐标为当，闸门自动打开，即第三章流体动力学基础3-1．检验不可压缩流体运动是否存在？[解]（1）不可压缩流体连续方程 （2）方程左面项；；（2）方程左面=方程右面，符合不可压缩流体连续方程，故运动存在。3-2．某速度场可表示为，试求：（1）加速度；（2）流线；（3）t=0时通过x=-1，y=1点的流线；（4）该速度场是否满足不可压缩流体的连续方程？[解]（1）写成矢量即（2）二维流动，由，积分得流线：即（3），代入得流线中常数流线方程：，该流线为二次曲线（4）不可压缩流体连续方程：已知：，故方程满足。3-3．已知流速场，试问：（1）点（1，1，2）的加速度是多少？（2）是几元流动？（3）是恒定流还是非恒定流？（4）是均匀流还是非均匀流？[解] 代入（1，1，2）同理：因此（1）点（1，1，2）处的加速度是（2）运动要素是三个坐标的函数，属于三元流动（3），属于恒定流动（4）由于迁移加速度不等于0，属于非均匀流。3-4．以平均速度v=0.15m/s流入直径为D=2cm的排孔管中的液体，全部经8个直径d=1mm的排孔流出，假定每孔初六速度以次降低2%，试求第一孔与第八孔的出流速度各为多少？[解]由题意；；······；式中Sn为括号中的等比级数的n项和。由于首项a1=1，公比q=0.98，项数n=8。于是 3-5．在如图所示的管流中，过流断面上各点流速按抛物线方程：对称分布，式中管道半径r0=3cm，管轴上最大流速umax=0.15m/s，试求总流量Q与断面平均流速v。[解]总流量：断面平均流速：3-6．利用皮托管原理测量输水管中的流量如图所示。已知输水管直径d=200mm，测得水银差压计读书hp=60mm，若此时断面平均流速v=0.84umax，这里umax为皮托管前管轴上未受扰动水流的流速，问输水管中的流量Q为多大？（3.85m/s）[解]3-7．图示管路由两根不同直径的管子与一渐变连接管组成。已知dA=200mm，dB=400mm，A点相对压强pA=68.6kPa，B点相对压强pB=39.2kPa，B点的断面平均流速vB=1m/s，A、B两点高差△z=1.2m。试判断流动方向，并计算两断面间的水头损失hw。 [解]假定流动方向为A→B，则根据伯努利方程其中，取故假定正确。3-8．有一渐变输水管段，与水平面的倾角为45º，如图所示。已知管径d1=200mm，d2=100mm，两断面的间距l=2m。若1-1断面处的流速v1=2m/s，水银差压计读数hp=20cm，试判别流动方向，并计算两断面间的水头损失hw和压强差p1-p2。[解] 假定流动方向为1→2，则根据伯努利方程其中，取故假定不正确，流动方向为2→1。由得3-9．试证明变截面管道中的连续性微分方程为，这里s为沿程坐标。[证明]取一微段ds，单位时间沿s方向流进、流出控制体的流体质量差△ms为因密度变化引起质量差为由于3-10．为了测量石油管道的流量，安装文丘里流量计，管道直径d1=200mm ，流量计喉管直径d2=100mm，石油密度ρ=850kg/m3，流量计流量系数μ=0.95。现测得水银压差计读数hp=150mm。问此时管中流量Q多大？[解]根据文丘里流量计公式得3-11．离心式通风机用集流器A从大气中吸入空气。直径d=200mm处，接一根细玻璃管，管的下端插入水槽中。已知管中的水上升H=150mm，求每秒钟吸入的空气量Q。空气的密度ρ为1.29kg/m3。[解] 3-12．已知图示水平管路中的流量qV=2.5L/s，直径d1=50mm，d2=25mm，，压力表读数为9807Pa，若水头损失忽略不计，试求连接于该管收缩断面上的水管可将水从容器内吸上的高度h。[解]3-13．水平方向射流，流量Q=36L/s，流速v=30m/s，受垂直于射流轴线方向的平板的阻挡，截去流量Q1=12L/s，并引起射流其余部分偏转，不计射流在平板上的阻力，试求射流的偏转角及对平板的作用力。（30°；456.6kN）[解]取射流分成三股的地方为控制体，取x轴向右为正向，取y轴向上为正向，列水平即x方向的动量方程，可得： y方向的动量方程：不计重力影响的伯努利方程：控制体的过流截面的压强都等于当地大气压pa，因此，v0=v1=v23-14．如图（俯视图）所示，水自喷嘴射向一与其交角成60º的光滑平板。若喷嘴出口直径d=25mm，喷射流量Q=33.4L/s，，试求射流沿平板的分流流量Q1、Q2以及射流对平板的作用力F。假定水头损失可忽略不计。[解]v0=v1=v2x方向的动量方程：y方向的动量方程： 3-15．图示嵌入支座内的一段输水管，其直径从d1=1500mm变化到d2=1000mm。若管道通过流量qV=1.8m3/s时，支座前截面形心处的相对压强为392kPa，试求渐变段支座所受的轴向力F。不计水头损失。[解]由连续性方程：伯努利方程：动量方程：3-16．在水平放置的输水管道中，有一个转角的变直径弯头如图所示，已知上游管道直径，下游管道直径，流量m3/s，压强，求水流对这段弯头的作用力，不计损失。 [解]（1）用连续性方程计算和m/s；m/s（2）用能量方程式计算m；mkN/m2（3）将流段1-2做为隔离体取出，建立图示坐标系，弯管对流体的作用力的分力为，列出两个坐标方向的动量方程式，得将本题中的数据代入：=32.27kN=7.95kN33.23kN水流对弯管的作用力大小与相等，方向与F相反。3-17．带胸墙的闸孔泄流如图所示。已知孔宽B=3m，孔高h=2m，闸前水深H=4.5m，泄流量qV=45m3/s，闸前水平，试求水流作用在闸孔胸墙上的水平推力F，并与按静压分布计算的结果进行比较。 [解]由连续性方程：动量方程：按静压强分布计算3-18．如图所示，在河道上修筑一大坝。已知坝址河段断面近似为矩形，单宽流量qV=14m3/s，上游水深h1=5m，试验求下游水深h2及水流作用在单宽坝上的水平力F。假定摩擦阻力与水头损失可忽略不计。[解]由连续性方程： 由伯努利方程：由动量方程：4-2用式（4-3）证明压强差△p、管径d、重力加速度g三个物理量是互相独立的。解：===将、、的量纲幂指数代入幂指数行列式得=-20因为量纲幂指数行列式不为零，故、、三者独立。4-4用量纲分析法，证明离心力公式为F=kWv2/r。式中，F为离心力；M为作圆周运动物体的质量；为该物体的速度；d为半径；k为由实验确定的常数。解：设据量纲一致性原则求指数、、：M：1=L：1=T：-2=-解得=1=2=-1故4-6有压管道流动的管壁面切应力，与流动速度、管径D、动力粘度和流体密度有关，试用量纲分析法推导切应力的表达式。解：[解]由已知选择为基本量，m=3，n=5，则组成n-m=2个π项 将π数方程写成量纲形式解上述三元一次方程组，得解上述三元一次方程组，得代入后，可表达成即4-7一直径为d、密度为的固体颗粒，在密度为、动力粘度为的流体中静止自由沉降，其沉降速度，其中为重力加速度，-为颗粒与流体密度之差。试用量纲分析法，证明固体颗粒沉降速度由下式表示：解：选、、为基本量，故可组成3个数，即其中，求解各数，即对于，即对于， 即故=0化简整理，解出又与成正比，将提出，则4-8设螺旋浆推进器的牵引力取决于它的直径D、前进速度、流体密度、粘度和螺旋浆转速度。证明牵引力可用下式表示：解：由题意知，选为基本量，故可组成3个数，即其中，即对于即对于即故就F解出得4-10溢水堰模型设计比例=20，当在模型上测得流量为时，水流对堰体的推力为，求实际流量和推力。解：堰坎溢流受重力控制，由弗劳德准则，有，由==而所以，即4-13将高，最大速度 的汽车，用模型在风洞中实验（如图所示）以确定空气阻力。风洞中最大吹风速度为45。（1）为了保证粘性相似，模型尺寸应为多大？（2）在最大吹风速度时，模型所受到的阻力为求汽车在最大运动速度时所受的空气阻力（假设空气对原型、模型的物理特性一致）。解：（1）因原型与模型介质相同，即故由准则有所以，（2），又，所以即4-14某一飞行物以36的速度在空气中作匀速直线运动，为了研究飞行物的运动阻力，用一个尺寸缩小一半的模型在温度为℃的水中实验，模型的运动速度应为多少？若测得模型的运动阻力为1450N，原型受到的阻力是多少？已知空气的动力粘度，空气密度为。解：由准则有即所以（2）5-2有一矩形断面小排水沟，水深，底宽流速水温为15℃，试判别其流态。解：，>，属于紊流5-3温度为℃的水，以的流量通过直径为的水管，试判别其流态。如果保持管内液体为层流运动，流量应受怎样的限制？解：由式（1-7）算得℃时， （1）判别流态因为所以，属于紊流（2）要使管内液体作层流运动，则需即5-4有一均匀流管路，长，直径，水流的水力坡度求管壁处和处的切应力及水头损失。解：因为所以在管壁处：处：水头损失：5-5输油管管径输送油量，求油管管轴上的流速和1长的沿程水头损失。已知，。解：（1）判别流态将油量Q换成体积流量Q，层流（2）由层流的性质可知（3）5-6油以流量通过直径的细管，在长的管段两端接水银差压计，差压计读数，水银的容重，油的容重。求油的运动粘度。解：列1-2断面能量方程取（均匀流），则 假定管中流态为层流，则有因为属于层流所以，5-7在管内通过运动粘度的水，实测其流量，长管段上水头损失H2O，求该圆管的内径。解：设管中流态为层流，则而代入上式得验算：，属于层流故假设正确。5-9半径的输水管在水温℃下进行实验，所得数据为，，。（1）求管壁处、处、处的切应力。（2）如流速分布曲线在处的速度梯度为4.34，求该点的粘性切应力与紊流附加切应力。（3）求处的混合长度及无量纲常数如果令，则？解：（1）（2）（3）所以=又若采用，则5-10圆管直径，通过该管道的水的速度，水温℃。若已知 ，试求粘性底层厚度。如果水的流速提高至，如何变化？如水的流速不变，管径增大到，又如何变化？解：℃时，（1）（2）（3）5-12铸铁输水管长=1000，内径，通过流量，试按公式计算水温为10℃、15℃两种情况下的及水头损失。又如水管水平放置，水管始末端压强降落为多少？解：(1)t=10℃时，符合舍维列夫公式条件，因，故由式（5-39）有(2)t=15℃时，由式（1-7）得由表5-1查得当量粗糙高度则由式（5-41）得，5-13城市给水干管某处的水压，从此处引出一根水平输水管，直径，当量粗糙高度=。如果要保证通过流量，问能送到多远？（水温℃）解：t=25℃时，由式（5-41）得， 又由达西公式得5-14一输水管长，内径管壁当量粗糙高度，运动粘度，试求当水头损失时所通过的流量。解：t=10℃时，由式（1-6）计算得，假定管中流态为紊流过渡区因为代入柯列勃洛克公式（5-35）得㏒=-2㏒()所以=检验：因为,属于过渡区，故假定正确，计算有效。5-16混凝土排水管的水力半径。水均匀流动1km的水头损失为1m,粗糙系数，试计算管中流速。解：水力坡度谢才系数代入谢才公式得5-20流速由变为的突然扩大管，如分为二次扩大，中间流取何值时局部水头损失最小，此时水头损失为多少？并与一次扩大时的水头损失比较。解：一次扩大时的局部水头损失为：分两次扩大的总局部水头损失为：在、已确定的条件下，求产生最小的值: 即当时，局部水头损失最小，此时水头损失为由此可见，分两次扩大可减小一半的局部水头损失。5-21水从封闭容器沿直径，长度的管道流入容器。若容器水面的相对压强为2个工程大气压，，局部阻力系数沿程阻力系数，求流量。解：取基准面，列断面能量方程所以==Q==5-22自水池中引出一根具有三段不同直径的水管如图所示。已知，，，局部阻力系数求管中通过的流量并绘出总水头线与测压管水头线。解：取基准面，则断面方程得其中，5-23图中，，计算水银差压计的水银面高差，并表示出水银面高差方向。解：以为基准面，据又==7.65 5-25计算图中逐渐扩大管的局部阻力系数。已知，工程大气压，，工程大气压，，流过的水量。解：以断面为基准面，据又，==又'